Linear Vector Combination Problem,即线性向量组合问题。写这个其实是由前一篇 post 而来(从百鸡问题到数学思维)。
这篇 post 由以下几个部分构成
这里再将题目重复一下,“鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。百钱买百鸡,问鸡翁、母、雏各几何?”。
符号定义
那么我们令
\begin{equation}
V=\left[
\begin{array}
\vec{v_1}\\
\vec{v_2}\\
\vdots\\
\vec{v_n}
\end{array}
\right]
\tag{1}
\end{equation}
其中
\begin{equation}
\vec{v_i}=\left(
\begin{array}{}
p_1, p_2, \cdots, p_m
\end{array}
\right)
\tag{2}
\end{equation}
因此,\(V\)是一个\(n\times m\)的矩阵,其中每一行\(v_i\)都是一个\(m\)维向量,\(v_i\)里每一个分量\(p_j\)是第\(j\)个property。
例如在这道题里,我们有
\begin{equation}
V=\left[
\begin{array}{}
\vec{v_1}\\
\vec{v_2}\\
\vec{v_3}
\end{array}
\right]
=\left[
\begin{array}{Chicken}
5 & 1\\
3 & 1\\
1 & 3\\
\end{array}
\right]
\tag{3}
\end{equation}
对于\(\vec{v_1}=\left(5,1\right)\)来说,第一个分量\(p_1=5\)是价格这一项属性,第二个分量\(p_2=1\)是只数这一属性。
那么在具体的百元百鸡问题中,我们的目标向量是\(\vec{G}=\left(100,100\right)\),并且有一组常数组成的\(1\times n\)的矩阵\(C\)作为各\(v_i\)的系数
$$C=\left[\begin{array}{}c_1 & c_2 & \cdots & c_n\end{array}\right]$$
使得
\begin{equation}
CV=G
\tag{4}
\end{equation}
矩阵求法
在这个矩阵方程中,\(C\)是我们需要求的,\(V,G\)均是已知的量。因为这是一个很简单的矩阵方程,自然会想到像这样求出\(C\)
\begin{equation}
\begin{aligned}
CV&=G\\
CVV^{-1}&=GV^{-1}\\
C&=GV^{-1}
\end{aligned}
\tag{5}
\end{equation}
不过我们并不能确定矩阵\(V\)是否是方阵,所以需要先将矩阵\(V\)变换为方阵。再提一下,\(C\)是\(1\times n\)的,\(V\)是\(n\times m\),\(G\)是\(1\times m\)
这里假设有\(n\ge m\),于是给出如下解决办法
先从\(V\)中提出前\(n-m\)行,组成新的\((n-m)\times m\)矩阵
\begin{equation}
V'=\left[
\begin{array}{}
\vec{v_1}\\
\vec{v_2}\\
\vdots\\
\vec{v}_{n-m}
\end{array}
\right]
\tag{6}
\end{equation}
而原来的\(V\)则变成了一个\(m\times m\)的矩阵
\begin{equation}
V=\left[
\begin{array}{}
\vec{v}_{n-m+1}\\
\vec{v}_{n-m+2}\\
\vdots\\
\vec{v_n}
\end{array}
\right]
\tag{7}
\end{equation}
接下来,对矩阵\(C\)也做类似的事
\begin{equation}
C'=\left[
\begin{array}{}
c_1 & c_2 & \cdots & c_{n-m}
\end{array}
\right]
\tag{8}
\end{equation}
\begin{equation}
C=\left[
\begin{array}{}
c_{n-m+1} & c_{n-m+2} & \cdots & c_n
\end{array}
\right]
\tag{9}
\end{equation}
如此一来,\(C\)是\(1\times m\)的,而\(C'\)是\(1\times (n-m)\)
那么这样变换是为了什么呢?为了说明原因,我们暂时回到具体的问题上来,在百元百鸡问题中,
\begin{equation}
\begin{aligned}
&CV=G\\
&c_1(5,1)+c_2(3,1)+c_3(1,3)=G\\
&c_1(5,1)+c_2(3,1)+c_3(1,3)=(100,100)\\
&c_2(3,1)+c_3(1,3)=(100,100)-c_1(5,1)
\end{aligned}
\tag{10}
\end{equation}
这里等价于我们之前用一般方法化简时的一组等式
(当然,这里我们移动的项不同,但从本质上来说是等价的)
\begin{equation}
\label{spend-amount-variation}
\left\{
\begin{aligned}
5a+3b&=n-\frac{c}{3}\\
a+b&=n-c
\end{aligned}
\right.
\end{equation}
在有了上面的等式之后,我们会人工进行消去变量的操作,然后得到\(a,b\)关于\(c\)的表达式
在这里,或许已经能猜出来了,根据上面提到的的解决办法,我们有
\begin{equation}
\begin{aligned}
&\left\{\begin{aligned}
C &= \left[\begin{array}{}c_2 & c_3\end{array}\right]\\
C'&= \left[\begin{array}{}c_1\end{array}\right]\\
\end{aligned}\right.\\\\
&\left\{\begin{aligned}
V &= \left[\begin{array}{}3&1\\1&3\end{array}\right]\\
V'&= \left[\begin{array}{}5&1\end{array}\right]
\end{aligned}\right.
\end{aligned}
\tag{11}
\end{equation}
那么可以观察到,\(V'C'\)正好就是\(c_1(5,1)\),正好是和\(G=\begin{bmatrix}100 & 100\end{bmatrix}\)相同,是一个\(1\times 2\)的矩阵。那么我们可以对它们进行操作,并得到
\begin{equation}
\begin{aligned}
CV&=G-V'C'\\
CVV^{-1}&=(G-V'C')V^{-1}\\
C&=(G-V'C')V^{-1}
\end{aligned}
\tag{12}
\end{equation}
进行到这一步之后,我们一下就得到了\(c_2,c_3\)与\(c_1\)的关系。
放入题中则是
\begin{equation}
\begin{aligned}
CV&=G-V'C'\\
\begin{bmatrix}
c_2 & c_3
\end{bmatrix}
\begin{bmatrix}
3 & 1 \\
1 & 3
\end{bmatrix}&=
\begin{bmatrix}
100 - 5c_1 & 100 - c_1
\end{bmatrix}
\end{aligned}
\tag{13}
\end{equation}
接下来求出\(V^{-1}\)
\begin{equation}
\begin{aligned}
\begin{bmatrix}
3 & 1 \\
1 & 3
\end{bmatrix}^{-1} =
\frac{1}{8}
\begin{bmatrix}
3 & -1 \\
-1 & 3
\end{bmatrix}
\end{aligned}
\tag{14}
\end{equation}
同时右乘
\begin{equation}
\begin{aligned}
C&=(G-V'C')V^{-1}\\
\begin{bmatrix}
c_2 & c_3
\end{bmatrix}&=
\frac{1}{8}
\begin{bmatrix}
100 - 5c_1 & 100 - c_1
\end{bmatrix}
\begin{bmatrix}
3 & -1 \\
-1 & 3
\end{bmatrix}\\
&=\frac{1}{8}
\begin{bmatrix}
200 - 14c_1 & 200 + 2c_1
\end{bmatrix}\\
&=
\begin{bmatrix}
25 - \frac{7}{4}c_1 & 25 + \frac{1}{4}c_1
\end{bmatrix}
\end{aligned}
\tag{15}
\end{equation}
即
\begin{equation}
\left\{
\begin{aligned}
c_2 &= 25 - \frac{7}{4}c_1\\
c_3 &= 25 + \frac{1}{4}c_1
\end{aligned}
\right.
\end{equation}
再之后,根据限制条件即可算出来。
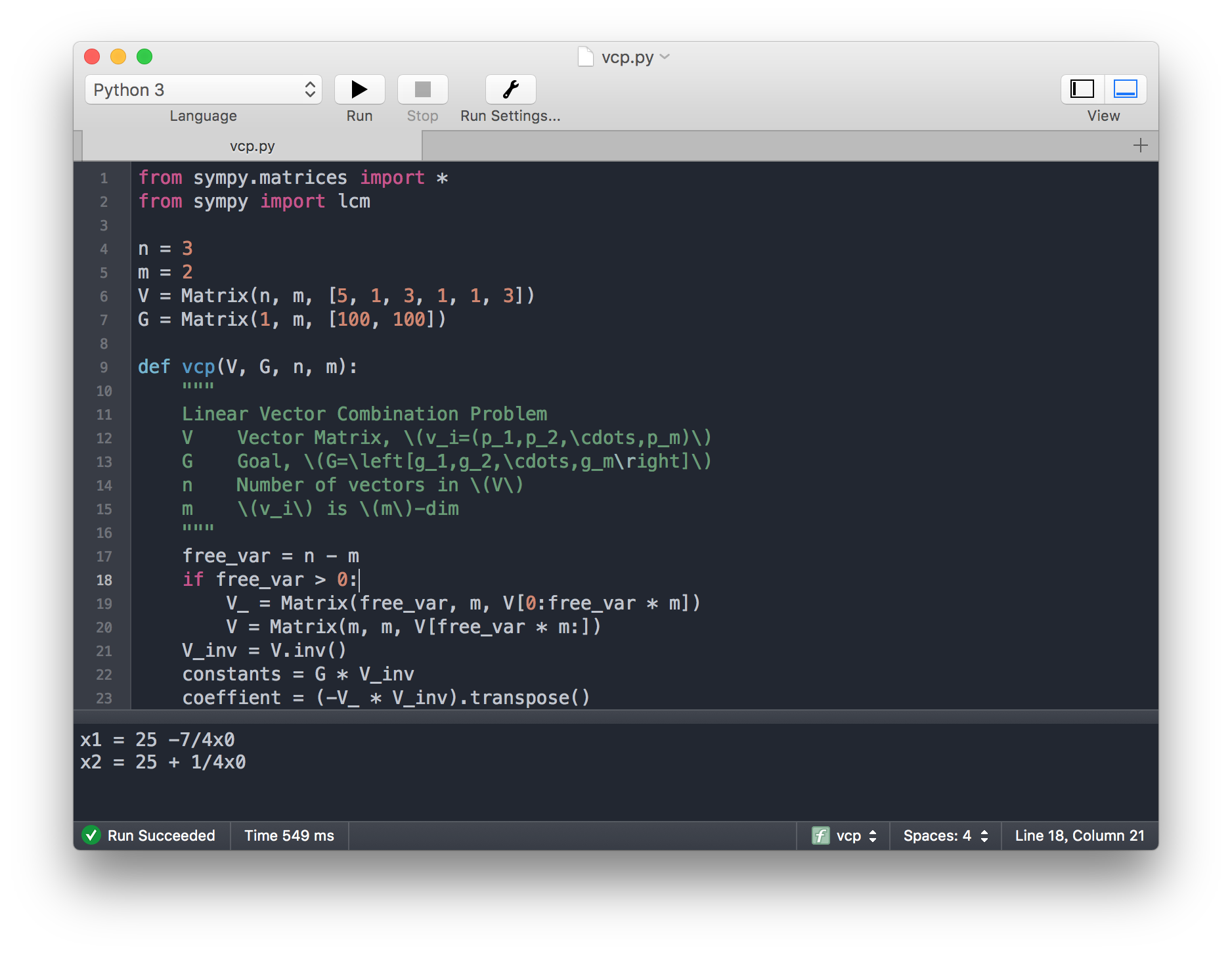
代码实现
from sympy.matrices import * n = 3 m = 2 V = Matrix(n, m, [5, 1, 3, 1, 1, 3]) G = Matrix(1, m, [100, 100]) def vcp(V, G, n, m): """ Linear Vector Combination Problem V Vector Matrix, \(v_i=(p_1,p_2,\cdots,p_m)\) G Goal, \(G=\left[g_1,g_2,\cdots,g_m\right]\) n Number of vectors in \(V\) m \(v_i\) is \(m\)-dim """ free_var = n - m if free_var > 0: V_ = Matrix(free_var, m, V[0:free_var * m]) V = Matrix(m, m, V[free_var * m:]) V_inv = V.inv() constants = G * V_inv coeffient = (-V_ * V_inv).transpose() non_free_var = len(constants) denoms = [[]] for i in range(non_free_var): print("x%d = %d" % (i + free_var, constants[i]), end='') for f in range(free_var): sign = '' fp = i*free_var+f if coeffient[fp] > 0: sign = '+ ' print(" %s%sx%d" % (sign, coeffient[fp], f), end='') if len(denoms) <= f: denoms.append([]) denoms[f].append(coeffient[fp].as_numer_denom()[1]) print('') vcp(V, G, n, m)
总结
那么用矩阵来做的意义是什么?比起人工计算变量间的关系,现在可以用计算机来做,特别是当\(n-m>1\)的时候,使用这种方法会减少不少人力。
另外这里的矩阵方法也回答了在一般解法中,“消去变量的意义是什么”这一问题,在线性代数中,如果我们有\(n\)个变量,但是却只有\(m\)个等式,这意味着我们有\(n-m\)个自由变量。因此,如果想要用矩阵求解,那么\(V\)必须是方阵,只有方阵才是可逆的,故选出\(n-m\)个自由变量,使得\(V\)是方阵。在经过矩阵运算之后,得到\(m\)个非自由变量与\(n-m\)个自由变量间的关系。